| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 오비탈
- TWRP
- 달빅캐시
- 커롬
- 선형조합 오비탈
- 분자 오비탈
- 베시업
- 시그마 결합
- cm12
- flashify
- 백업
- 파이결합
- tekcafe
- miui
- LCAO
- 베가
- 루팅
- bolbbalgan4
- 캐시
- 결합길이
- 결합차수
- 정리장
- ios
- 커스텀롬
- 플래싱
- flyme
- 부트로더
- cyanogenmod
- 오비탈 믹싱
- IMEI
- Today
- Total
목록전체 글 (16)
정리장
오랜만에 작업한 악보 입니다. 볼사를 좋아하는 만큼 마음을 담아 만들었어요. 그냥 반주를 넣기보다 원곡과 비슷하게 하려고 노력한 것 같습니다. This is the sheet music download link! 즐 피아노 하세요! 시험기간에 뭐하고 있는..?
 샤오미 LED 스탠드 개봉기& 리뷰, 기대만큼 큰 아쉬움
샤오미 LED 스탠드 개봉기& 리뷰, 기대만큼 큰 아쉬움
이제 며칠 후에 기숙사에 들어가는데, 거기에 스탠드가 필요하답니다.집에 있는 스탠드는 매우 낡아서.. ㅋ(이따가 사진 참조) 굉장히 세련된 제품으로 구입을 했죠. 이름하여 샤오미 LED '스마트' 스탠드.LED라고 해서 다 같은 LED가 아닌데요, 우리나라는 60Hz를 쓰니 60Hz로 깜박이는 LED가 있고 그렇지 않은 LED가 있어요. 확인법은 스마트폰 카메라를 켜고 LED 등에 검은 줄이 연속적으로 나타나는지 여부를 확인하시면 됩니다. (플리커 프리 말하는 겁니다)이 리뷰를 보실 분들은 이미 제원표를 확인하셨을테니 스펙은 넘어가구요,http://www.wemakeprice.com/deal/adeal/3203740/못보신 분들은 여기서 확인하세요~ 자 이제 개봉기로 넘어갑시다.일단 박스가 이렇게 왔어요..
 #5 분자 오비탈(LCAO, MO)
#5 분자 오비탈(LCAO, MO)
[서문]안녕하세요 정리장 입니다. 다음의 글은 대학교 (일반) 과학을 다루고 있습니다. (고등학교 2과정과 비슷합니다) 이 링크의 글을 먼저 읽어보시면 이해하시기 수월할껍니다.http://schrodingerpiano.tistory.com/notice/11 [본문]목차 1. LCAO와 MO 2. 결합 차수, 결합 길이, 자성1. LCAO와 MO 선형조합 오비탈과 분자 오비탈이라 부른다.이런거다. 이해가 잘 안갈 수도 있으니 다른 그림을 첨부하겠다. 호오, 그런거구나. H원자 2개가 있다고 상상해보자. 이 두개가 결합을 하려한다. 근데 얘네는 결합하면서 따로 흡열이나 발열반응을 하지 않는다. 일단 활성화 에너지를 주면 결합을 형성하고, 근데 따로 흡열이나 발열을 하지 않기때문에 결합 한 에너지 만큼 반결합..
 #4 혼성오비탈
#4 혼성오비탈
[서문]안녕하세요 정리장 입니다. 다음의 글은 대학교 (일반 화학/생물) 과학을 다루고 있습니다. (대학과학은 고등학교 2과정과 비슷합니다) 이 링크의 글을 먼저 읽어보시면 이해하시기 수월할껍니다.http://schrodingerpiano.tistory.com/notice/11 [본문]몇마디 덧붙이자면, 화학에서 이미 몇 개의 글을 써버린 관계로 양자화학이 끝난 후에야 쌍극자 모멘트, 기/액/고체 등의 파트를 넣을 수 있을 것 같다.(이미 써놓았으나 올리지 못함) 그리고 이번 글은 전글과 전전글에 대한 내용이 없으면 이해가 안되니 주의할 것(시그마/파이 결합, VSEPR과 입체수)1. 혼성화 다른말로 혼성 오비탈. 입체수에 따라 결정되는 요인이다. 이를 이해하기 위해 베릴륨(Be)이 결합하는 방법을 알아..
[서문]안녕하세요 정리장 입니다. 다음의 글은 대학교 (일반 물리/화학/생물 등) 과학을 다루고 있습니다. 이 링크의 글을 먼저 읽어보시면 이해하시기 수월할껍니다.http://schrodingerpiano.tistory.com/notice/11 [본문]1. VSEPR과 입체수 여느 책에 나와있는 것처럼 VSEPR을 먼저 하지 않는 이유는 VSEPR에서 파이결합에 대한 내용이 나오기 때문이다. VSEPR은 원자가 전자쌍 반발이론, 즉 원자 하나당 비공유/공유 전자쌍에 대한 이론이다. 이 이론은 특정 '입체수'에 따라 분자의 분자구조를 결정하는 역할을 한다. 그럼 입체수가 무엇이냐, 결합/비결합 개수를 세는 것이다. 이때, 결합의 경우는 시그마 결합만 세고 파이결합은 세지 않는다. 정확하지는 않지만 그 이유..
 #2 시그마 결합, 파이결합
#2 시그마 결합, 파이결합
[서문]안녕하세요 정리장 입니다. 다음의 글은 대학교 (일반 물리/화학/생물 등) 과학을 다루고 있습니다. 이 링크의 글을 먼저 읽어보시면 이해하시기 수월할껍니다.http://schrodingerpiano.tistory.com/notice/11 [본문]1. 시그마 결합과 파이결합 누가 고맙게도 줌달 화학책에 있는 사진을 그대로 스캔했다. 출처는 구글 이미지. 사진에 있는 sp라는 단어는 다음시간에 뭔지 자세히 배우므로 신경쓰지 말자. 다음은 C2H4를 나타내는 구조다. 여기서 시그마 결합은 C와 C 사이에 직접 작용하는 것이다. 직접이니 중간에 초록색 두개를 맞대고 있는게 시그마 결합이라는 거다. 그리고 파이결합은 두 C 원자에서 두개의 오비탈이 서로 상호작용 하는 것이다. 파이결합이 일어나는 이유는 2..
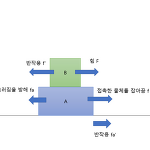 #4 장력, 탄성력, 마찰력
#4 장력, 탄성력, 마찰력
[서문]안녕하세요 정리장 입니다. 다음의 글은 대학교 (일반 물리/화학/생물 등) 과학을 다루고 있습니다. 이 링크의 글을 먼저 읽어보시면 이해하시기 수월할껍니다.http://schrodingerpiano.tistory.com/notice/11 [본문]목차: 1. 장력 2. 탄성력 3. 정지마찰력 4. 운동마찰력 1. 장력 정의: 실/줄이 양쪽 물체를 당기는 힘 특징: 질량=0, 팽팽한 줄 에서만 장력이 성립한다. 특성: 탄성력의 일종으로 용수철 저울에 나타나는 무게도 장력 힘을 전달해주는 역할을 한다. 활용: B의 알짜힘은 F-T 이고 A의 알짜힘은 T이다. 이때 m=M이라면 T=F-T, 즉 F=2T에 해당한다. F=ma이므로 A의 m 값이 커지면 F값도 커지는데 이는 a를 같게 유지하기 위해서다. A..
 #3 뉴턴의 운동법칙
#3 뉴턴의 운동법칙
[서문]안녕하세요 정리장 입니다. 다음의 글은 대학교 (일반 물리/화학/생물 등) 과학을 다루고 있습니다. 이 링크의 글을 먼저 읽어보시면 이해하시기 수월할껍니다.http://schrodingerpiano.tistory.com/notice/11 [본문]목차 1. 관성 2. 알짜힘 3. 관성의 법칙, 가속도의 법칙 5. 작용-반작용의 법칙 1. 관성 정의: 물체의 원래 운동상태를 유지하려는 성질 특징: 변화에 대한 저항; 운동의 요인이 됨 (힘과는 다름) 특성: 관성의 크기는 질량이다. 활용: 운동의 정의는 시간에 대한 위치 변화율이다. 이는 속도의 정의와 같다. 물체의 원래 운동상태를 유지하려는 성질을 가지고 있다는 것은 정지속도를 유지하려 하는 성질을 가지고 있다는 말과 같다. 관성기준계에 대해 50k..
 #2: 차원과 운동
#2: 차원과 운동
[서문]안녕하세요 정리장 입니다. 다음의 글은 대학교 (일반 물리/화학/생물 등) 과학을 다루고 있습니다. 이 링크의 글을 먼저 읽어보시면 이해하시기 수월할껍니다.http://schrodingerpiano.tistory.com/notice/11 [본문]목차 1. 차원 2. 변위 3. 속도 4. 가속도 5. 상대운동 6. 등가속도 운동 7. 포물선 운동1. 차원 정의: 같은 물리학적 성질을 가지는 것들을 분류하기 위한 방법 특징: 질량을 M, 길이를 L, 시간을 T로 하여 유도단위를 다음과 같은 꼴로 나타냄 $$[M^a L^b T^c]$$ 특성: MLT(질량 길이 시간)계가 있고 FLT(힘 길이 시간)계가 있음 활용: 밀도의 차원: $$[M^-1 L^3] \quad ( 부피=길이^3 /질량)$$2. 변위 ..
 #1 벡터와 스칼라
#1 벡터와 스칼라
[서문]안녕하세요 정리장 입니다. 다음의 글은 대학교 (일반 물리/화학/생물 등) 과학을 다루고 있습니다. 이 링크의 글을 먼저 읽어보시면 이해하시기 수월할껍니다.http://schrodingerpiano.tistory.com/notice/11 [본문]목차 1. 스칼라 2. 벡터1. 스칼라 정의: 크기만을 가진 양 특징: 사칙연산이 가능 특성: (-) 값도 스칼라임 (예 - 온도 등) 고등과정에서 기하와 벡터 전까지의 모든 연산은 스칼라량2. 벡터 정의: 크기와 방향을 가진 양 특징: 사칙연산이 불가 특성: (행렬로 벡터를 표현하다니) 1) 평행이동 - $$\begin{matrix} \nearrow & \rightarrow & \nearrow \end{matrix}$$ 벡터의 덧셈 뺄셈에서 주로 쓰임 2..
